• Home
• Research
• Projects
• Patents
• Press
• Demos
• Code
• Teaching
• Talks
• People
• Contact
• CV
• Music
Patents
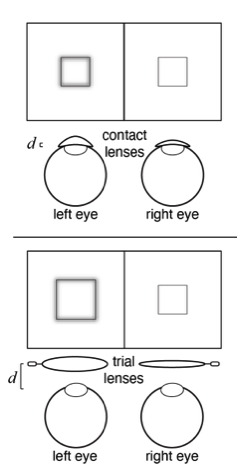
Imaging systems (e.g. cameras) often require accurate, automatic, and fast estimates the lens' focus error. Maximally accurate focus error estimates are obtained by first calculating the pattern of contrast at each level of detail (i.e. spatial frequency) in individual natural image patches (e.g. 64x64 pixels). Next, using Bayesian statistics, we determine how probable each focus error is by comparing the contrast pattern in each patch to contrast patterns that are characteristic of different focus errors. The characteristic patterns depend on the properties of the imaging system's optics, sensors, and noise. They characteristic patterns also depend on the properties of imaged natural scenes. In a typical smart phone camera, chromatic aberrations can be used to correctly estimate the sign of the error 98% of the time. Estimates are accurate, precise, and can be computed in ~1 millisecond.

Natural
Scenes
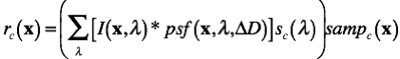
Optics

Sensor
Sampling
Sensor
Sensitivity
Licensing Inquiries
Data
Optimal focus error estimation performance for the optics of a Samsung Galaxy phone.
• Burge J & Geisler WS (2014). Optimal focus error estimation performance in individual images of a popular smart phone.
Technical Document, University of Texas at Austin. [ pdf ]
Patent documents
• Burge J, Geisler WS (Dec. 2013) An image-based method for the optimal estimation of defocus in individual natural
images. U.S. Patent Publication No. US-2013-0329122-A1 [ pdf ]
• Burge J, Geisler WS (Feb. 2011) An image-based method for the optimal estimation of defocus in individual natural
images. U.S. Provisional Patent 22084-P069.
Relevant publications
• Burge J & Geisler WS (2012). Optimal defocus estimates from individual images for autofocusing a digital camera.
Proceedings of the SPIE, 8299, 82990: E1-E12, January: Burlingame, CA [ pdf ] (Best Paper Award!)
• Burge J, Geisler WS (2011). Optimal defocus estimation in individual natural images. Proceedings of the National
Academy of Sciences, 108 (40): 16849-16854 [ pdf ]
Focus Error Estimation from Individual Images
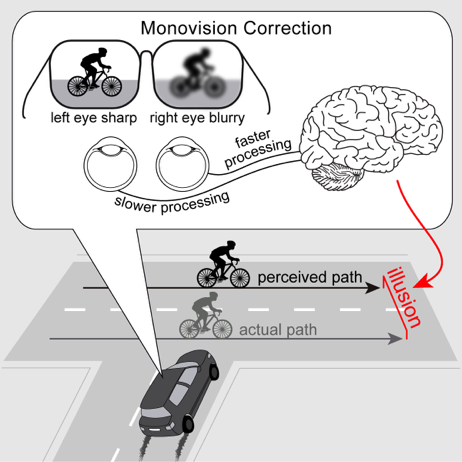
We have recently reported a new motion illusion--the reverse Pulfrich Effect--caused by monovision corrections, a lens prescription for presbyopia currently in use by millions. Presbyopia is the age-related condition that causes all people over age 50 to lose the ability to focus their eyes. Reading glasses, bifocals, and progressive lenses are the most widely known remedies. Monovision is another common but less well-known correction that is typically implemented with contact lenses or surgical methods. With monovision, each eye is corrected to focus light from a different distance, causing one image to be blurrier than the other. The brain suppresses the blurrier image and preferentially processes the sharper one, thereby expanding the depth of field. Monovision is known to decrease stereoacuity, but it is not known how interocular differences in blur impact motion perception. We show that interocular blur differences can cause people to dramatically misperceive the distance and 3D direction of moving objects. When driving, for example, distance may be misperceived by the width of a lane of traffic! The illusion occurs because the interocular differences in blur cause interocular mismatches in processing speed. For moving objects, the mismatch in processing speed results in a neural disparity, which leads to the illusory percepts. Using non-invasive techniques, we measured how blur differences affect neural processing times with sub-millisecond precision. Most importantly, we have shown that individualized measurements paired with clever application of existing ophthalmic technologies can eliminate the illusion in a large important subset of viewing conditions. Our discoveries may lead to new lines of premium lenses for presbyopes, a population that is soon expected to reach 2 billion worldwide.
Anti-Pulfrich Monovision Ophthalmic Corrections
Patent documents
• Burge J, Rodriguez-Lopez V, Dorronsoro C. Anti-Pulfrich monovision ophthalmic correction.
U.S. Provisional Application No. 62/799,468. Filing date: January 31, 2019.
Relevant publications
• Burge J, Rodriguez-Lopez V, Dorronsoro C (2019). Monovision and the misperception of motion.
Current Biology, 29 (15), 2586-2592 doi: https://doi.org/10.1016/j.cub.2019.06.070 [ html1 | html2 | pdf ]
Licensing Inquiries